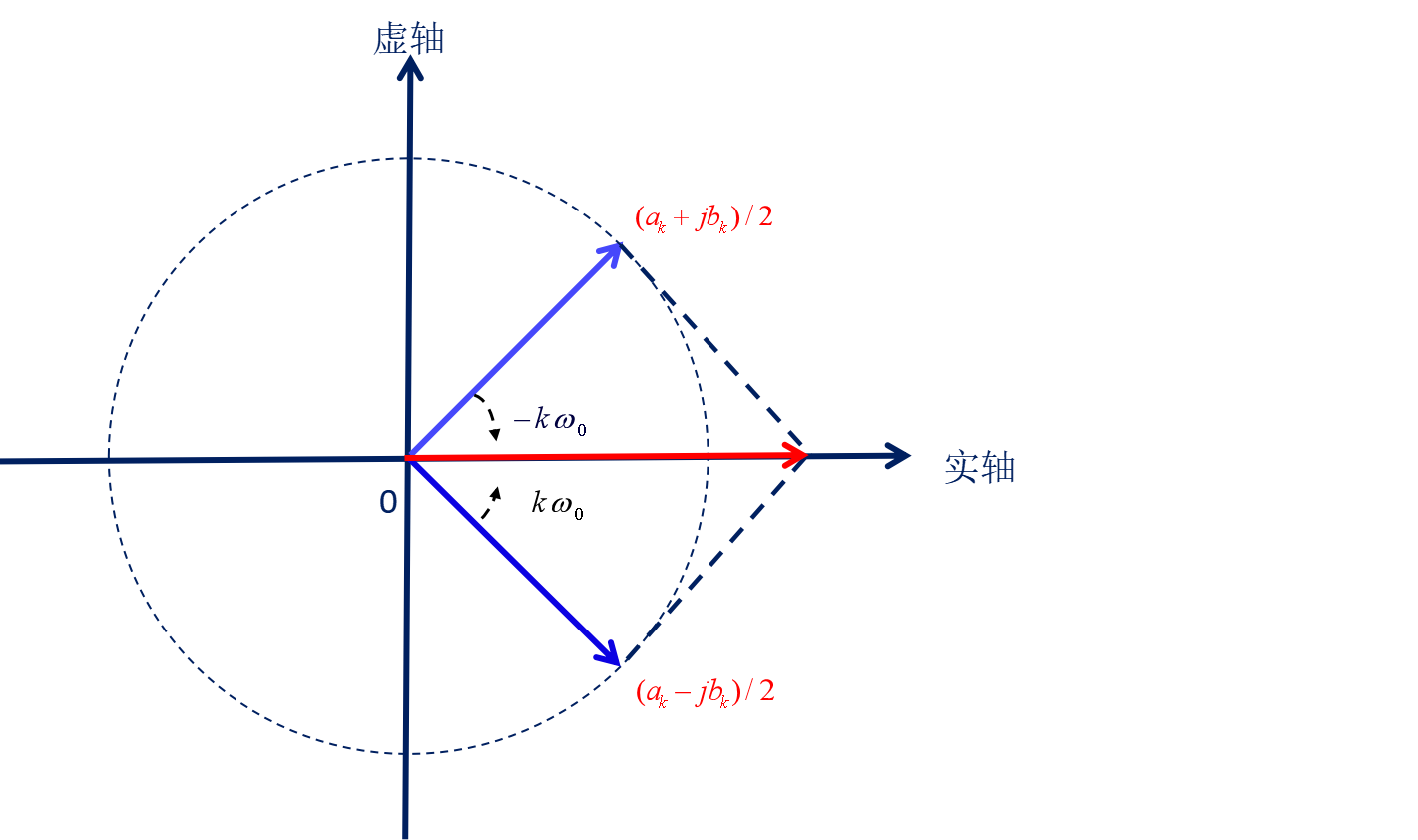$$\qquad$$注：图中蓝色的向量即代表复傅立叶系数，即t=0时刻旋转向量所在的位置。

$$\qquad$$注意两点： $$\qquad$$1、由于初始相位关于实轴对称，旋转角速度相同，旋转方向相反，合并后的旋转向量只在实轴上有分量， 在虚轴上没有分量。得到这样的结论是因为：我们分析的信号本身是实信号。 $$\qquad$$2、正负频率对应的复傅立叶系数合并，是向量相加，不是简单的幅度相加。

$$\qquad$$从前面的分析来看，虽然我们通过复傅立叶级数展开将实信号分解为了一系列的旋转向量之和（由此引出了复数，使得实信号的表达式中出现了复数），但由于逆时针和顺时针旋转的向量成对出现，而且成对出现的旋转向量的初始相位关于实轴对称，旋转的角速度相同，旋转方向相反，所以这些旋转向量合成的结果最终还是一个实信号（只在实轴上有分量，虚轴上的分量相互抵消掉了）。