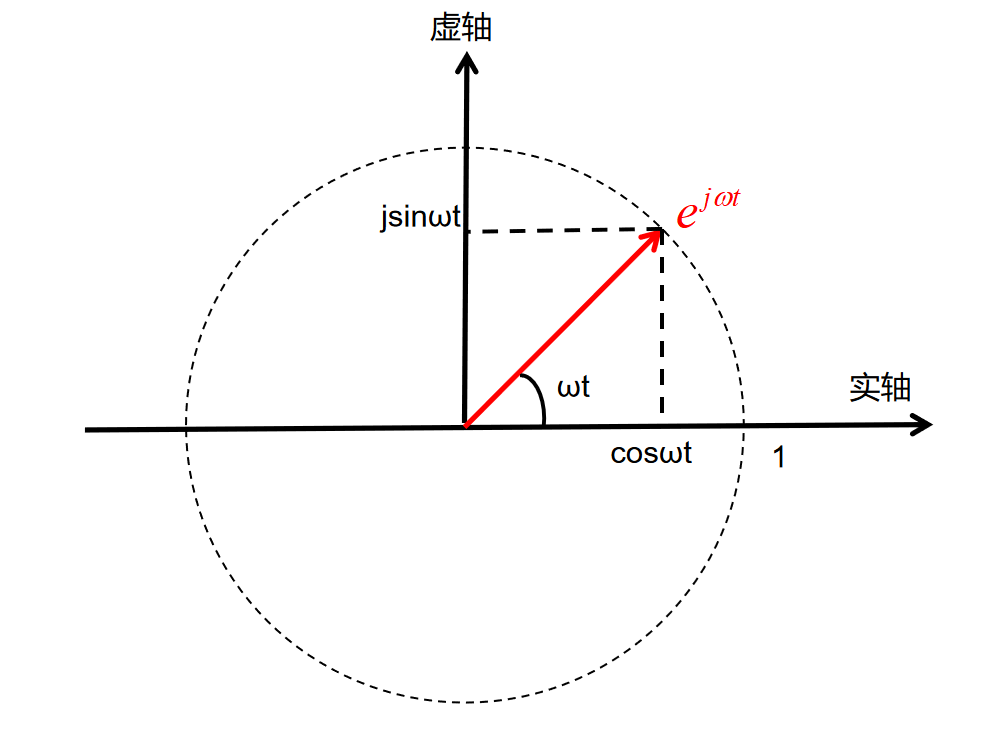
加上时间轴t，我们来看旋转向量的三维图：

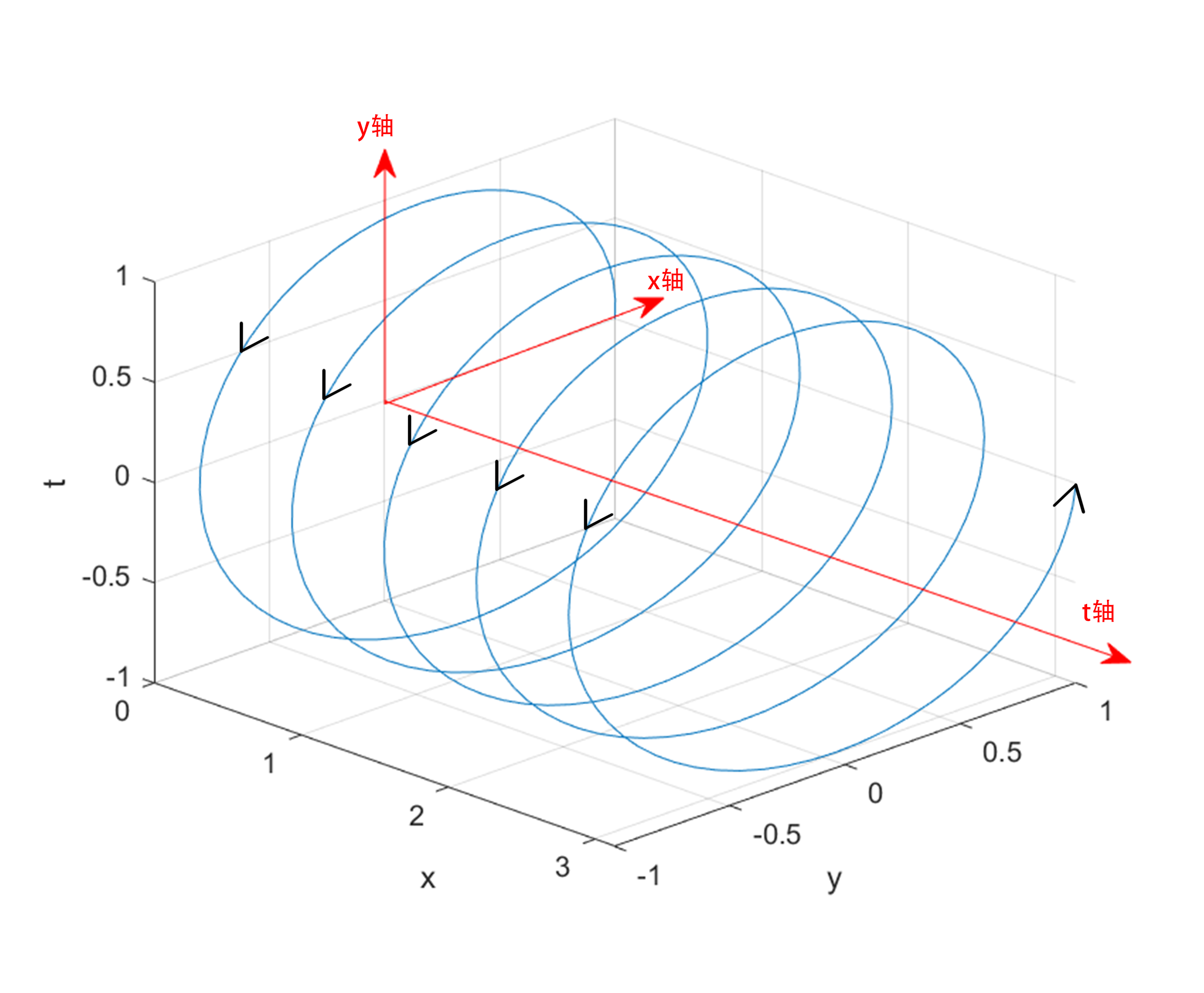
% 定义螺旋线参数
t = 0:0.1:10*pi; % 参数t，从0到10π，表示螺旋线会转10圈
r = 1; % 螺旋线的半径
k = 0.1; % 螺旋线在z轴上的增长率

% 计算螺旋线的x, y, z坐标
x = r * cos(t);
y = r * sin(t);
z = k * t;

% 绘制螺旋线
plot3(z, x, y);
hold on; % 保持当前图形，以便添加更多的图形元素

% 设置坐标轴的标签
xlabel('x');
ylabel('y');
zlabel('t'); % 注意在你的图中是使用t而不是通常的z

% 设置图形的视角
view(45, 30);

% 开启网格
grid on;

% 关闭保持状态
hold off;

注：x轴为实轴，y轴为虚轴

旋转向量在x-y平面的投影：

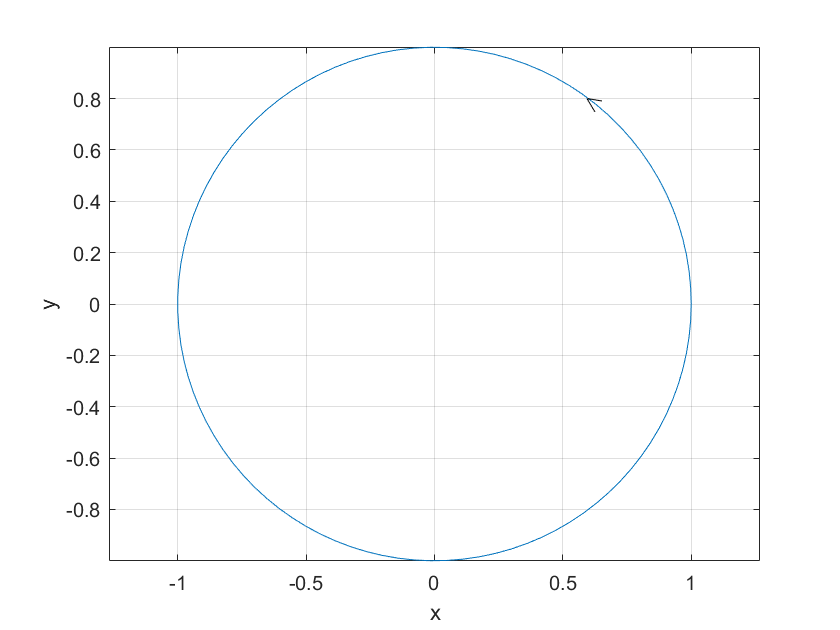
theta = linspace(0, 2*pi, 100); % 生成100个点来画圆
x = cos(theta);
y = sin(theta);

plot(x, y); % 画出单位圆
axis equal; % 确保x轴和y轴的刻度一致
grid on; % 显示网格
xlabel('x');
ylabel('y');
title('单位圆');

旋转向量在x-t平面的投影：

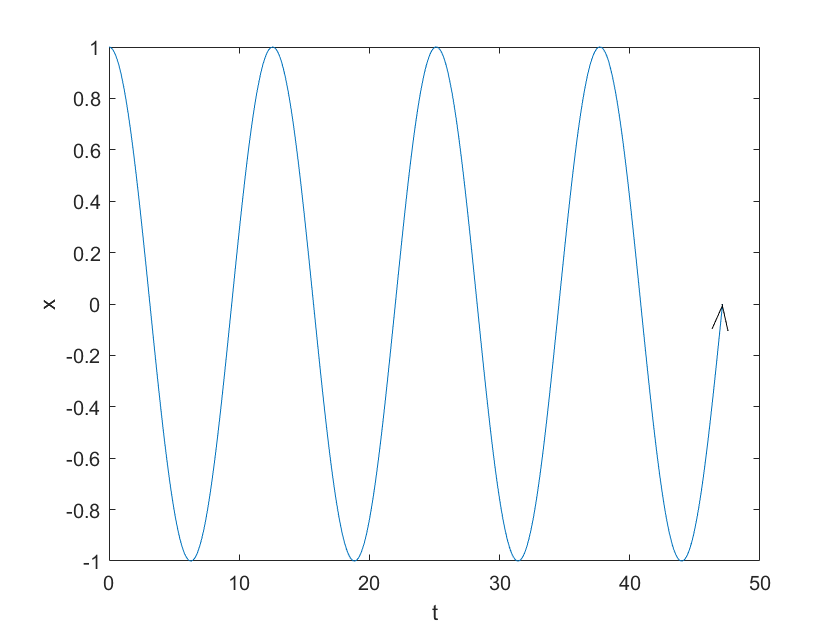
theta = linspace(0, 15*pi, 1000); 
x = cos(theta/2);
plot(theta,x) ; 
axis ([0,50,-1,1]); 
xlabel('t');
ylabel('x');

旋转向量在y-t平面的投影：

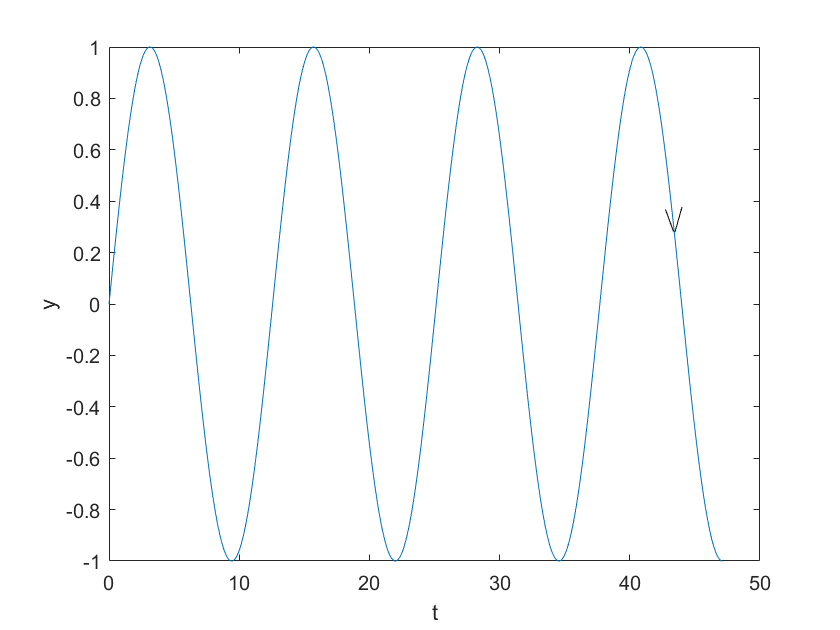
theta = linspace(0, 15*pi, 1000); 
y = sin(theta/2);
plot(theta,y) ; 
axis ([0,50,-1,1]); 
xlabel('t');
ylabel('y');